Increasingly FPGAs are being used to perform signal-processing tasks, particularly in computationally demanding application areas such as video processing and communications. Their massive parallelism often allows FPGAs to handle data rates much higher than what DSPs and general-purpose processors can manage, and in today’s world of rapidly evolving applications and standards FPGAs’ programmability is an advantage over hard-wired solutions. In recent years FPGA vendors have begun to include signal-processing-oriented features such as hard-wired multiplier units in their chips, making FPGAs an even more appealing solution for many DSP applications.
But implementing an algorithm on an FPGA requires much greater design effort compared to a DSP or general-purpose processor. Efficient FPGA implementations involve many subtle design choices and complex tradeoffs. In addition, the languages and tools traditionally used for FPGA design are unfamiliar to most DSP engineers. Fortunately, FPGA vendors and several tools vendors now provide high-level tools aimed at implementing signal processing algorithms on FPGAs while maintaining an intuitive representation of the algorithm. In this article we explore how these offerings help developers meet the challenges of using FPGAs in signal processing applications.
Describing DSP algorithms
Signal processing algorithms are often designed and specified using the The MathWorks’ MATLAB language or via a graphical block diagram language using tools such as The MathWorks’ Simulink. (See “Languages for Signal Processing Software Development” for more on this topic.)
But carefully optimized implementations of signal processing algorithms targeting FPGAs have historically taken the form of RTL code. This code bears little resemblance to the abstract, intuitive block diagram descriptions or MATLAB code.
FPGA vendors and independent tools vendors provide FPGA development tools that help bridge this gap between an intuitive algorithm description and an optimized implementation. Most of these tools rely on the popular Simulink and MATLAB languages to represent signal-processing algorithms and provide features to enable FPGA implementation from these high-level descriptions.
Like most block-diagram languages, Simulink allows users and third-party vendors to provide customized blocks that users can incorporate into algorithm designs. FPGA vendors and FPGA tool vendors typically provide libraries of Simulink blocks representing common signal processing functions such as filters, FFTs, and error correction encoders and decoders. When users develop their algorithms using only these special blocks, the FPGA tools can convert the design into an FPGA implementation. FPGA market leaders Xilinx and Altera both provide such Simulink libraries and associated tools. Xilinx’s offering is System Generator; Altera’s is DSP Builder.
Third-party tools such as Synplicity’s Synplify DSP follow the same trend, but provide technology independence: Synplify DSP can target any FPGA or ASIC from its Simulink block library, while tools from Xilinx and Altera are specific to these vendors’ chips. Rather than providing its own custom block libraries, FPGA vendor Lattice Semiconductor relies on Synplify DSP to support implementation on its FPGA devices from a Simulink-based design.
Graphical block diagram languages have their advantages, but some algorithm developers prefer to use the MATLAB language for its powerful matrix and vector manipulation capabilities. Tool vendor AccelChip provides tools for converting algorithm descriptions in MATLAB into synthesizable RTL code that can easily be implemented in an FPGA or ASIC. AccelChip also provides a link to Xilinx’s Simulink-based System Generator environment, allowing users to convert MATLAB code into a block that can be incorporated into a Simulink block diagram and synthesized with System Generator.
Other tool vendors prefer to use their own languages instead of relying on MATLAB or Simulink. For example, CoWare’s SPW employs its own graphical block diagram language. SPW is oriented toward system-level design, where different portions of the system—such as a channel equalizer or error correction coder—may be implemented using different technologies, such as FPGAs, DSPs, or ASICs.
Since tools based on MATLAB or graphical block diagram languages rely on libraries of common DSP blocks, typically they are only effective in applications that are built primarily from common DSP functions.
The C language is also commonly used to describe DSP algorithms, particularly in standards-based applications. For example, C reference code is available for video compression standards such as MPEG-4 and H.264. Tools from vendors such as Celoxica assist designers in converting C code to an optimized FPGA implementation.
The challenges of FPGA-based implementation
Implementing signal processing algorithms on an FPGA in an efficient manner requires many subtle design choices and tradeoffs. Tools that target FPGA implementations from abstract, high-level algorithm descriptions must therefore allow the user to explore implementation tradeoffs. A key challenge for these tools is the need to allow users to control a variety of implementation details while keeping the algorithm and implementation descriptions as intuitive and abstract as possible.
One significant difference between an abstract algorithm description and an algorithm implementation is that the implementation must specify the precision of arithmetic operations. Algorithms are often designed using floating-point arithmetic. This provides more than sufficient precision for the vast majority of applications and allows considerations about the precision of specific variables or operations to be ignored. But implementing floating-point arithmetic in an FPGA is almost always an inefficient approach. Therefore creating an optimized implementation of an algorithm described using floating-point arithmetic requires conversion to fixed-point arithmetic, and FPGA tools provide features to support this conversion.
Although Simulink primarily uses floating-point arithmetic, The MathWorks provides fixed-point arithmetic modeling for Simulink, enabling conversion of algorithms to fixed-point implementation. In addition, fixed-point simulation capabilities for MATLAB are available from The MathWorks and from Catalytic. However, tools from Xilinx and Altera opt to perform fixed-point arithmetic within the blocks of their Simulink libraries independently of Simulink’s own fixed-point arithmetic support. In contrast, Synplicity’s Synplify DSP builds on Simulink’s fixed-point modeling and analysis capabilities. Synplify DSP also features automatic data type propagation, allowing the user to specify the desired precision only at key points in the DSP algorithm. Synplify DSP then attempts to automatically determine appropriate fixed-point data types and widths throughout the design.
AccelChip’s DSP synthesis tool also attempts to automatically determine appropriate fixed-point data types throughout the design. Unlike Synplify DSP, however, AccelChip’s AutoQuantizer feature uses test vectors provided by the designer to empirically measure the dynamic range of each variable in the design. Using this information, the tool can assign fixed-point data types to variables.
Automated analyses can greatly reduce the effort of converting an algorithm to fixed-point. But in most applications, additional analysis and guidance by an experienced user is needed in order to obtain a fixed-point implementation that is both functional and efficient.
Some of the most challenging choices and tradeoffs that designers must make when implementing signal processing algorithms on an FPGA involve the design of an appropriate data path architecture for each portion of the algorithm. FPGAs provide great flexibility for the user to implement diverse signal-processing data path architectures. FPGA users must choose between conventional arithmetic or “distributed arithmetic” (DA) techniques, determine appropriate levels of pipelining and parallelism, and decide how to buffer data. These types of choices are subject to complex routing and timing constraints and affect performance, cost, and power consumption. As a result, designing an optimal data path to implement a signal processing function on an FPGA can be extremely challenging.
FPGA vendors’ tools address this optimization challenge by providing parametric IP blocks for most common signal processing functions. For example, Altera provides an “FIR Compiler” that automatically generates efficient FIR filter implementations for various Altera FPGAs, given user-specified parameters such as the number of filter taps, the desired precision, and the level of parallelism. Similar tools are available from other FPGA vendors and from tool vendors such as AccelChip. These parametric IP blocks typically map closely to the corresponding blocks in these vendors’ Simulink block libraries. For example, an FIR filter block in a Simulink block diagram can be efficiently implemented in an FPGA by extracting the parameters from the Simulink FIR filter block and applying the same parameters to the FIR filter IP block. Figure 1 illustrates this approach to synthesizing FPGA implementations from Simulink block diagrams.
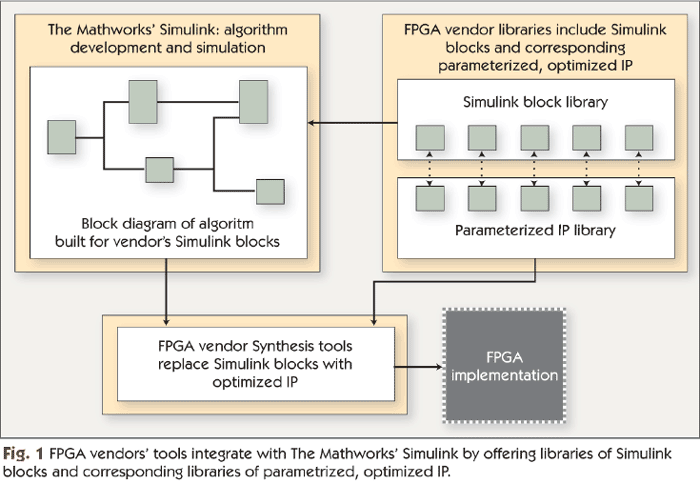
Mapping algorithm blocks to parametric IP is an effective approach in that efficient implementations are generated for individual blocks and tradeoffs between performance and area can be balanced throughout the algorithm. However, this approach severely limits the ability to optimize across block boundaries. For example, combining two blocks in order to share hardware resources such as hardwired multipliers would require implementing both blocks at the register transfer level, eliminating the benefits of the parametric IP blocks.
In contrast, Synplicity’s Synplify DSP applies optimizations at the algorithm level. For example, Synplify DSP is capable of “folding” the design, which shares hardware resources and automatically inserts the required multiplexers. Synplify DSP also automates architectural exploration. The user can specify data rates and area and timing constraints, and Synplify DSP attempts to make appropriate design choices and generate a suitable implementation.
Another interesting feature of Synplify DSP is the ability to generate a multi-channel implementation from a single-channel representation of an algorithm. Synplify DSP can automatically duplicate the design for multiple channels and then apply optimizations to the multi-channel implementation such as sharing of hardware resources between channels. This unique feature can greatly simplify optimization in multi-channel applications.
While FPGAs are increasingly used to implement signal-processing data paths, FPGAs are not generally used to implement the complex control flows found in some signal processing applications. Although it is possible to implement such functionality on an FPGA in the form of sophisticated finite state machines, designing these state machines can be an arduous and error-prone process. In many applications, FPGAs are paired with DSPs or general-purpose processors so that the control flow can be described as C code and delegated to these programmable processors. Some FPGA families include programmable processors within the FPGA fabric, allowing a similar partitioning of data path and control processing in a single-chip solution. For example, FPGAs in the Xilinx Virtex-4 family include up to two PowerPC processor cores.
Another common solution to this problem is to implement a simple programmable processor in the FPGA and then program this processor to implement the application’s control flow. FPGA vendors facilitate this by providing simple processor cores as IP blocks.
Final thoughts
Today’s tools have the potential to greatly simplify implementing signal-processing algorithms on FPGAs compared to traditional FPGA tools and design methodologies. Such tools are especially appealing to designers of large and complex applications where development effort is greatest. But working at a high level of abstraction always requires some sacrifices in efficiency—even the best tools generally can not exploit the sorts of creative fine-grained optimizations that expert designers can conceive. However, in today’s applications optimization at the register transfer level is not always practical due to the associated design effort. The high-level tools discussed in this article may make it practical to implement very complex and sophisticated signal-processing algorithms on FPGAs—if they can produce efficient enough implementations to meet the applications’ area, power, and speed constraints. We can expect the quality and capabilities of these tools to increase even further as FPGA vendors strive to capture more of the DSP application market.

Add new comment